[통계] 왜도와 첨도 파이썬으로 구현하기

멋쟁이 사자처럼 AI스쿨 9일차

: 수치형 데이터 EDA

 

비대칭도(왜도)

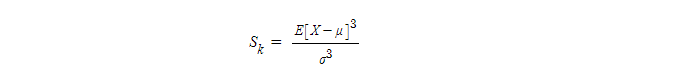
• 실수 값 확률 변수의 확률 분포 " 비대칭성 " 을 나타내는 지표
• 왜도의 값은 양수나 음수가 될 수 있으며 정의되지 않을 수도 있음
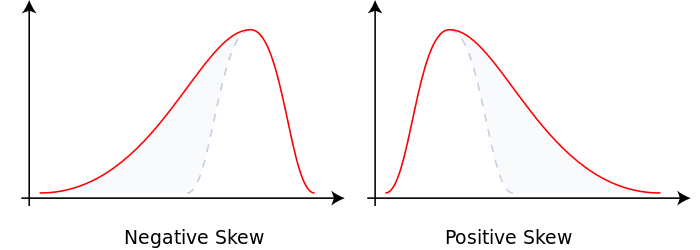
  • 왜도 < 0 일 경우. 확률밀도함수의 왼쪽 부분에 긴 꼬리를 가지고 중앙값을 포함한 자료가 오른쪽에 더 많이 분포
  • 왜도 > 0 일 경우, 확률밀도함수의 오른쪽 부분에 긴 꼬리를 가지며 자료가 왼쪽에 더 많이 분포
  • 왜도 = 0 일 경우, 평균과 중앙값이 같음

 

[ Python ]

# 평균과 분산 
def mean(lst):
    return sum(lst)/len(lst)

def var(lst):
    avg = mean(lst)
    result = 0
    for i in lst:
        result += (i - avg) ** 2
    return result/len(lst)

 

def skewness(lst):
    size = len(lst)
    result =  [((i - mean(lst))/var(lst)**0.5) **3 for i in lst]
    return sum(result)/size

 

inp1 =[1, 1, 1, 1, 1, 1, 2, 3, 4, 5]
inp2 = [1, 2, 3, 4, 5, 6, 6, 6, 6, 6]

skewness(inp1),skewness(inp2)

 

(1.060660171779821, -0.7680464255426254)

 

 

첨도

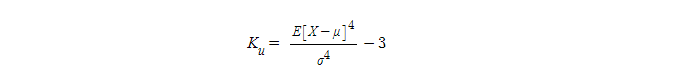
• 확률분포의 " 뾰족한 정도 "를 나타내는 척도
• 관측치들이 어느 정도 집중적으로 중심에 몰려 있는가를 측정할 때 사용
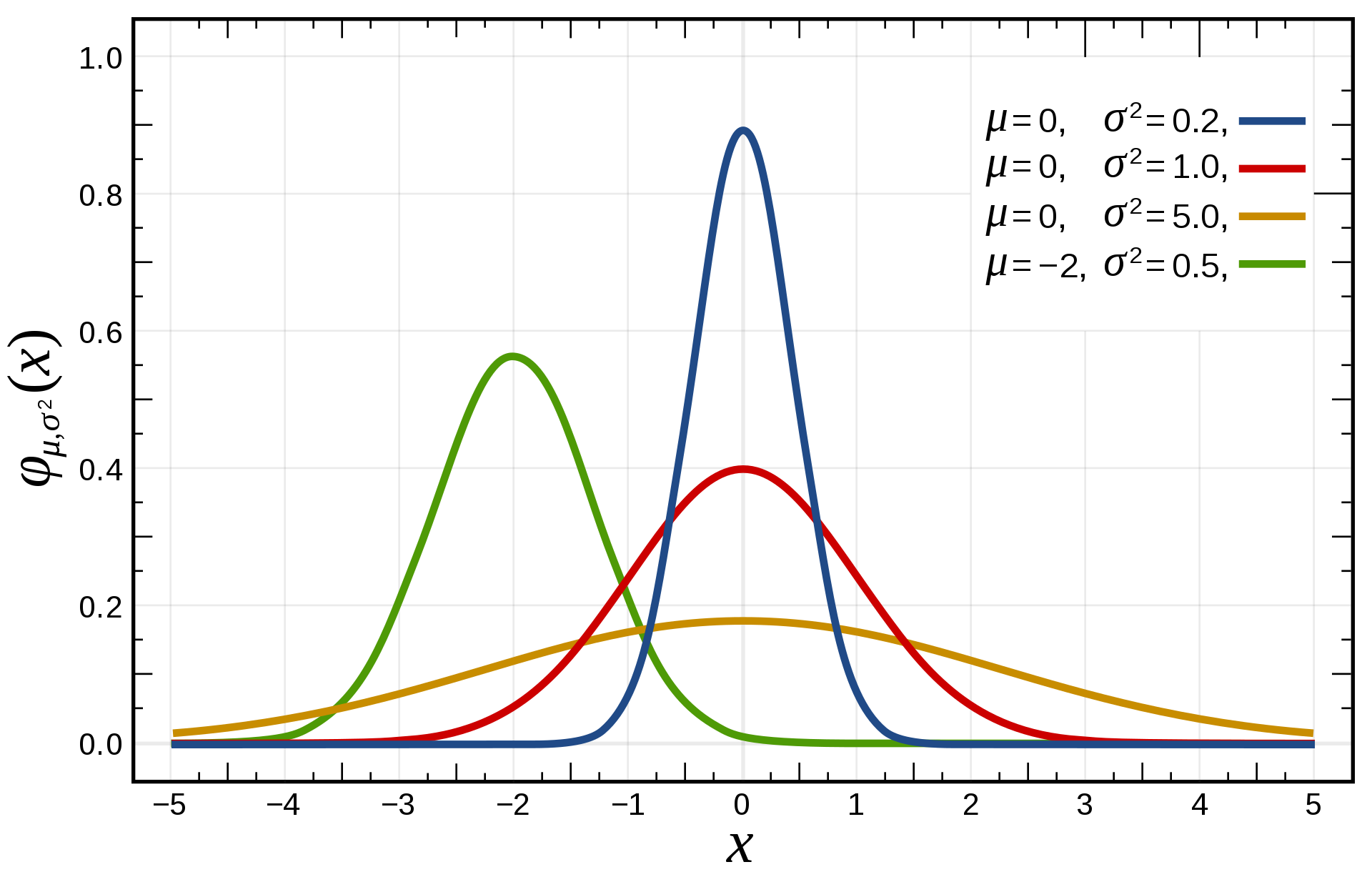
  • 첨도값(K)이 3에 가까우면 산포도가 정규분포에 가까움
  • 3보다 작을 경우에는(K<3) 산포는 정규분포보다 더 뾰족한 분포(꼬리가 얇은 분포)
  • 첨도값이 3보다 큰 양수이면(K>3) 정규분포보다 더 완만한 납작한 분포(꼬리가 두꺼운 분포)

[ Python ]

# 평균과 분산
def mean(lst):
    return sum(lst)/len(lst)

def var(lst):
    avg = mean(lst)
    result = 0
    for i in lst:
        result += (i - avg) ** 2
    return result/len(lst)

 

def kurtosis(lst):
    size = len(lst)
    result = [((i - mean(lst))/var(lst)**0.5) ** 4 for i in lst]
    return sum(result)/size -3

 

inp1 = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
inp2 = [1, 2, 3, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,  5, 5, 5, 5, 6, 7, 8, 9, 10]

kurtosis(inp1),kurtosis(inp2)

 

(-1.2242424242424241, 2.3518870698951044)

 

 

 

Reference

http://ds.sumeun.org/?p=885

pbj0812.tistory.com